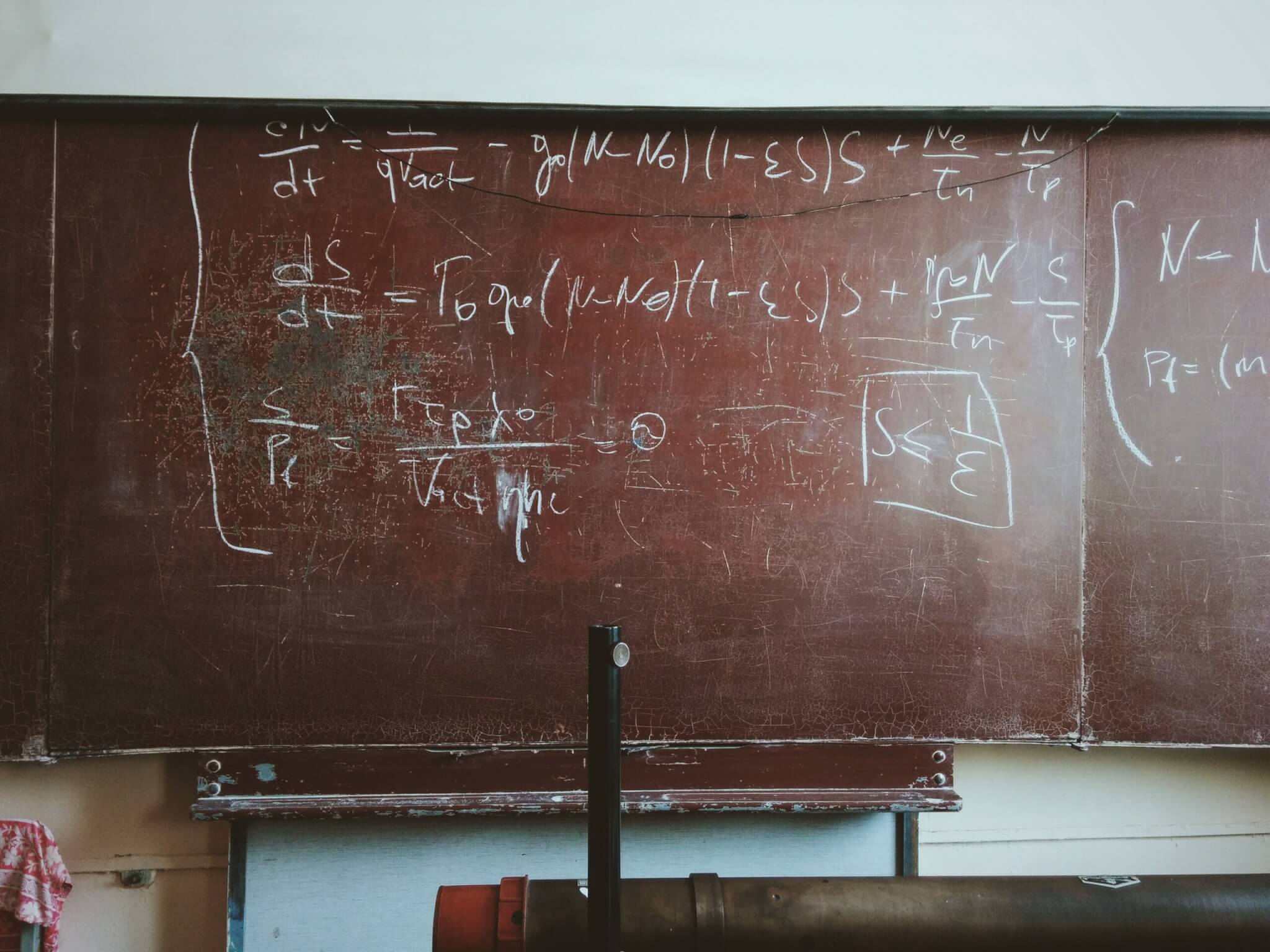
Are stories and parables told only through words?
Perhaps some might grant that parable-like tales are also told through visual art and music. I’d like to suggest, in addition, that there are many math – and, by logical extension, science – “parables” most of us have never heard. And even if we’ve heard them, many of us have likely overlooked the radically fantastic domain they represent and reflect.
The primary reason for this, sadly, is that few of us were told them as bedtime stories (though somewhat tongue in cheek, I’m actually quite serious about this).
We certainly weren’t likely to hear them in school, where the presentation of mathematical fact almost by diktat seems to require the gravitas of “very serious factual stuff”; it certainly doesn’t have the slightest thing to do with the “stuff and nonsense” of tall tales and mystical musings, right?
Most of us have at least heard of Little Red Riding Hood and Jack and the Beanstalk. Perhaps others have ventured further into the realm of fables like MacDonald’s The Princess and the Goblin. But I’d wager many of us were never told The Fable of the Fearsome √2. That’s a great shame, because the truth is, the stories that math tells us are every bit as interesting, suspenseful, beautiful, and yes, edifying, as good old-fashioned fairytales; and they can be every bit as awe-inspiring, quite possibly stupefying, and spiritually stimulating as the finest parables.
In short, many of us tend to regard mathematics as mechanistic and mundane, ignoring the fact that the ultimate conclusions of mathematics lead us to ideas in physics which we’re far from able to reduce to “mere” matter, and which are as wonderfully bewildering as the deepest questions of philosophy and theology (also ignoring the fact that lively and fanciful books have been written, such as Flatland, The Phantom Tollbooth, Alice in Wonderland, and A Wrinkle in Time, that should give us a clue that the world of math is teeming with delightful fancies and even a few suspenseful mysteries).
The truth about mathematics – and this is a fabulous revelation when it is grasped — could not be more stunning.
By way of explanation, let me begin with the concept of literacy. As classical educators, we recognize that we don’t teach reading and writing for the telos, or final purpose, of “functional” literacy. We reject the notion that the full purpose of learning to be literate in language is to master the steps to follow in a recipe or to successfully take a driver’s test and correctly interpret road signs (note how in recent years those written directions have been increasingly replaced by pictures, symbols, and now, videos; so if that was the purpose, it was a moot one).
I think it is safe to say that classical educators adamantly argue that the purpose of language literacy is a much higher one, one that meets a deeper need: to endow the recipient of this education with the skills, abilities, knowledge, and discernment to have holistic access to some of the highest works of creation to which people have aspired; to expose the student to writing that captures what it means to be human in the fullest, most illuminating senses; to bring him or her written words that can be guideposts and comforts to all who must confront our lives lived out in the human condition.
Classical educators also uphold the wonder of the epiphanies brought to us through the written word. It can hold our hands as a friend might, leading us – oh, so much more gently than experience in the “real” world often does – to the very threshold of truth, goodness, beauty, and beyond.
A classical educator recognizes that teaching a young child to read and write is a first step towards introducing him, not to the technical manual for a toaster oven, but to the inherited wealth of humanity’s written record of what it means to exist – the profoundest question, and the one that men and women have struggled with from the dawn of time. It also means giving him the ability to write his own contributions to the question. The somewhat simultaneous step of introducing a child to the world of fairytales, stories, poetry, and the narratives of history is yet another way in which we aim to prepare her to go through a fantastical portal into a wide experience of encountering and comprehending the humane, the self, the world, and the Creator. It also equips her with the capacity to express her own experience.
Classical educators need to recognize that, similarly, we ought not to teach mathematics simply for the functional literacy of balancing a checkbook, measuring a room for paint or wallpaper, or figuring out what the best price per ounce for strawberry jam is at the grocery store. These are useful skills. But they are not the telos of a mathematics education. Remember that arithmetic and geometry are an integral part of the liberal arts, along with harmony (music) and astronomy. As John of Salisbury wrote in his 12th century Metalogicon: “Mathematics rides [proudly] along on the four-wheel chariot of its Quadrivium, intermingling its fascinating demonstration in manifold variety.”
Also remember that mathematics is an incarnation of logic, and is one of the clearest ways of practicing ordered, lucid, and accurate thought processes, thereby instilling good discernment in our thinking habits. Antoine Arnauld claimed in The Art of Thinking: “Precision of thought is essential to every aspect and walk of life . . . Men are everywhere confronted with alternative routes — some true and some false — and reason must choose between them. Who chooses well has a sound mind . . . Capacity for discerning the truth is the most important measure of men’s minds. Our principle task is to train the judgment, rendering it as exact as we can.” Mathematics helps us do this. (1)
Above and beyond that, classical educators need to realize that the telos of mathematical literacy, though it may seem so in content and form, isn’t actually that different from that of language literacy. The similarity between these two is the subject of this article and those that follow.
The key to the answer lies in recognizing that mathematics is also a language – to my mind, it just has a different alphabet (as music does). It describes. It communicates. It tells stories about what we call “realities,” such as Newton’s mechanical forces, further developed by Faraday, Maxwell, and Einstein in gravitational and electromagnetic fields. Mathematical equations are sentences. Some are statements, some are questions, and some are answers. The equation which tells us that 2 + 2 = 4 (at least in base ten) is a statement. The equations that contain variables (the famous “unknowns” of algebra) pose questions. (2)
The answers, like Maxwell’s equations for electricity and magnetism or Einstein’s equation for general relativity, somehow express truths that give us access to the profoundest characteristics of the creation, especially its rationality (that is, its “being in sync” with human reason). That these equations are quite likely imperfect and imprecise in their descriptions of the ways of the universe is countered powerfully by the fact that they work. This is not a claim in favor of utilitarianism, but an assertion that the very utilitarianism of math is a testimony to its potency as a language describing “reality.” Mathematics is certainly a linguistic convention, but it must be more than that, because, as James Nickel puts it, “If mathematics is just a linguistic convention, then why are these conventions so useful in the real world?” (Mathematics: Is God Silent?)
This recognition goes further than acknowledging that a mathematical equation is basically the equivalent of a “predicate nominative” grammatical structure in spoken and written language (for example, recalling fondly a nursery rhyme for children: Little Miss Muffet is a girl who sits on a tuffet; or, more precisely, Miss Muffet = tuffet-sitter, this being the syllogistic form such a statement would take in Logic). It means acknowledging that classical teachers need to perceive the world of mathematics in much the same way they approach literature.
Consider “childish” (though they are no such thing) fairytales. What makes most contemporary education dismiss them, and even go so far as regard them as harmful (recall, for example, a rather pitiful Eustace’s attitude, gleaned from what Lewis calls his “advanced and up-to-date” parents and school, toward stories in The Voyage of the Dawn Treader)? The fact that fairytales contain creatures which are “not real” is frequently the basis of such dismissal. Don’t people often refer to fairytales as “made up”? The math and science fields that espouse “factual actuality” have many, usually quite vocal, advocates who reject the poor, maligned fairytale because it is fabricated: It is “imaginary.”
Exactly right here, in this word “imaginary,” we have arrived at the point of this article: This is where we encounter a wonderful parable-like quality of mathematics. Recollect that in the classification of numbers, there is an entire group of interesting entities that aren’t exactly numbers as we usually understand them, yet are part of our number systems and are frequently used in calculations. What are these called? “Imaginary” numbers! (3)
Wait, did I type that right? “Imaginary”? Did you read that right – did you read it with the idea that words have meaning and therefore the fact that they are called “imaginary” might have denotations and connotations that deserve further contemplation? (4)
Think of the fairytale-like creature called Euler’s ι (iota, or more commonly seen as “i,” the “imaginary unit”) which is equal to √-1. I’m pretty sure I can have no more depth of understanding of what √-1 is than I do about Tom Bombadil’s Goldberry, the River-woman’s daughter.
You see, the solution to x2 = -1 can be √-1 x √-1 = -1. This √-1 is therefore an extraordinarily rebellious fellow, who breaks the well-regarded order in which one can have a negative square root of x (-√x) but never a square root of negative x (√-x); this follows the rule that the square root of any number multiplied by itself equals itself, but breaks the rule that the product of two negative numbers must be a positive number . . . not to mention the fact that if we follow the mathematical rules for such things to their conclusions we end up with a big “no-no” in logic, a contradiction in which 1 = -1. A thing cannot be equal to itself and not itself at the same time!
Yet, through an ingeniously brilliant mathematical slight-of-hand, by representing the imaginary unit not as a square root but as a mathematical entity wearing a special transformative robe (that is, dressed up as a Greek iota), we use Euler’s ι with crazy abandon in mathematical sentences . . . excuse me, equations . . . in the form of so-called “complex numbers.” In doing so, we do lots of math literacy jumping jacks. In fact, we use this mysterious mathematical creature (one could even think of this wee iota as a mischievous, yet helpful, sprite) within such STEM giants (pun intended) as fluid dynamics, electrical engineering, and fractal geometry. (5)
Wait . . . what?
Do we understand who and what these “imaginary” numbers are any better than we understand what the house elf Dobby, the monster Grendel, or the nymph Kalypso might be? I believe the answer is: No.
Join me next time to continue exploring the mystifying and fabulous topography of mathematics in the second article in this topic, “Welcome to the World of Hyper-Sur-Reality.” It’s a risky mathematical world out there. As children will readily tell us that the fairytale universe is filled with dimly understood hazards, so we’d do well to remember why the number six was afraid . . . because seven eight nine, of course.
(Special thanks to James Nickel, author of Mathematics: Is God Silent? and the forthcoming math textbook The Dance of Number, for graciously providing feedback for this article as well as comments, which have been included as endnotes.)
Endnotes
- It also sets the limits of Logic, by Gödel’s Incompleteness Theorem. This points to the ground of mathematics as extra-logical.
- “An equation poses a mathematical ‘whodonit.’ The culprit x – the unknown x – left clues in the form of an equation, and the mathematical detective must determine its identity, the root (or roots) of the equations.” Donald C. Benson, A Smoother Pebble: Mathematical Explorations (2003), p. 128.
- The term “imaginary” was coined by Descartes; Cardano referred to them as “sophistic negatives” or “fictae,” while Newton’s term for them was “impossible.”
- Entire books, not textbooks, have been written to exposit the history and application of imaginary numbers: (a) Mazur, Barry. Imaging Numbers (particularly the square root of minus fifteen). New York: Farrar, Straus, and Giroux, 2003. (b) Nahin, Paul J. An Imaginary Tale: The Story of . Princeton: Princeton University Press, 1998.
- The Dance of Number [2018] Part 2, Volume 2, p. 713): In 1980, Loren Carpenter (1947-), a computer graphics researcher for the airplane manufacturer Boeing, developed a fractal algorithm called Reyes rendering that the Pixar animation studio eventually used for all their films. The infinite algorithms that generate these images capture the subtle design of mountains, landscapes, oceans, clouds, trees, shrubs, animals, people, movement, indeed, every aspect of created reality. Isn’t it stunning that the ingenuity of man can nearly duplicate, in animation form, the ingenuity of the Triune Creator?
